整合營銷服務商
電腦端+手機端+微信端=數據同步管理
免費咨詢熱線：
電腦端+手機端+微信端=數據同步管理
免費咨詢熱線：
我們介紹了兩組連續變量比較時t檢驗和非參數檢驗的選擇，今天我們再深入解釋下t檢驗的兩個重要適用條件——正態性和方差齊性吧。
我們先回顧一下，常用的t檢驗包括單樣本t檢驗、獨立樣本t檢驗和配對樣本t檢驗，它們都是對樣本均數（或樣本差值的均數）進行統計推斷。其各自適用條件可以參考表1。
表1 常見t檢驗的適用條件
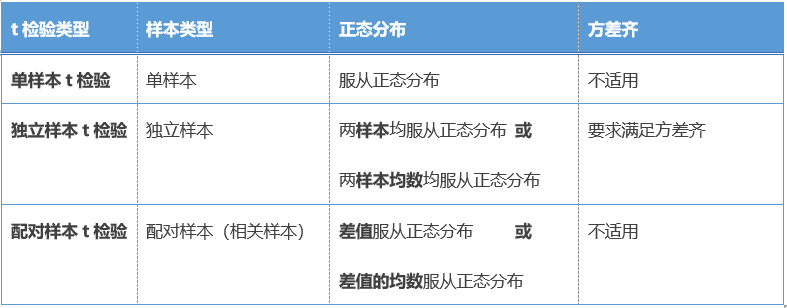
第二列中樣本類型的判定，已經介紹過了，感興趣的小伙伴可以前去查看。
回歸本期正題。對于正態性的要求，獨立樣本t檢驗與配對樣本t檢驗的區別在于一個看兩樣本是否都服從正態分布，一個看兩樣本差值是否服從正態分布。接下來為了簡單起見，我們以獨立樣本t檢驗為例。
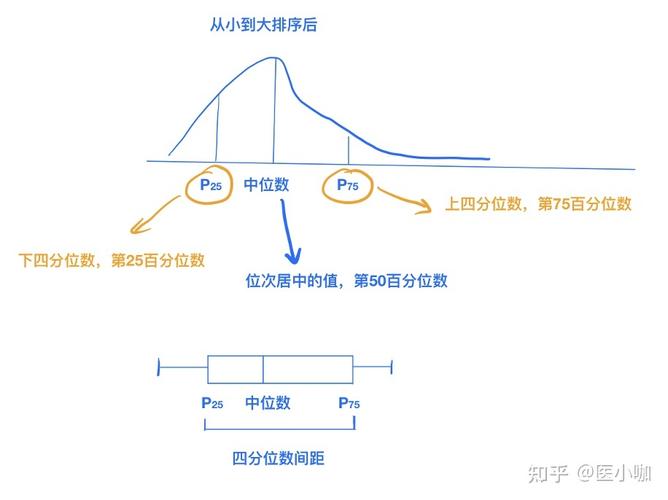
從表中我們不難發現，獨立樣本t檢驗要求“樣本來自正態分布總體”或“樣本均數服從正態分布”。第一種表述『樣本來自正態分布總體』其實是第二種表述『樣本均數服從正態分布』的一種特殊情況。當總體本身符合正態分布時，從這個總體里面隨機抽取的樣本的均數就一定服從正態分布了。
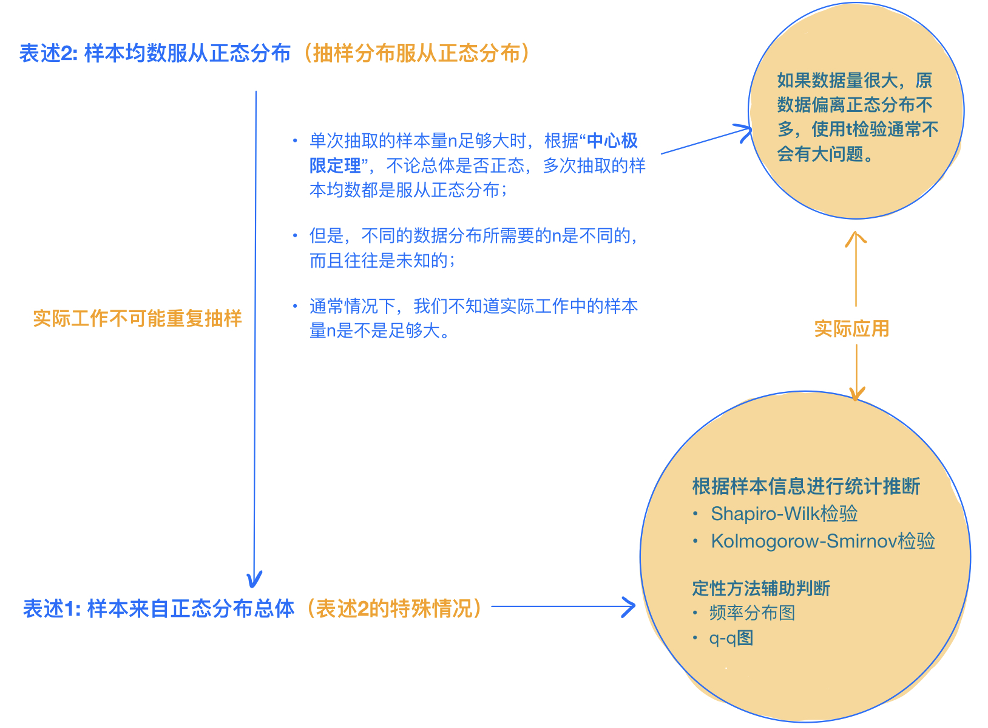
此外，這樣的差異表述源于實際研究工作的需要。實際工作中不可能無限重復抽取樣本來了解第二種表述，即『樣本均數服從正態分布』。因此，對于一次抽樣來說，可以通過樣本所能提供的信息進行統計推斷，判定樣本是否來自正態分布的總體，如使用Shapiro-Wilk或-Smirnov檢驗進行統計推斷；也可以采用定性的方法輔助判斷，如頻率分布圖、q-q圖。
對于第二種表述『樣本均數服從正態分布』，雖說當單次抽取的『樣本量n足夠大』時，根據『中心極限定理』，不論總體是否正態，多次抽取的樣本均數都服從正態分布，那么，這種情況下都可以使用t檢驗。但是，不同的數據分布所需要的n是不同的，而且往往是未知的，總體數據分布與正態分布偏離越大，樣本均數服從正態分布所需n越大，通常情況下，我們不知道實際工作中的樣本量n是不是足夠大。因此，使用第一種表述，即『樣本來自正態分布總體』還是會更保險一些。但實際應用中呀，如果數據量很大，原數據偏離正態分布不多，使用t檢驗通常不會有大問題。以上內容是關于正態性。
接下來我們再看看方差齊性：
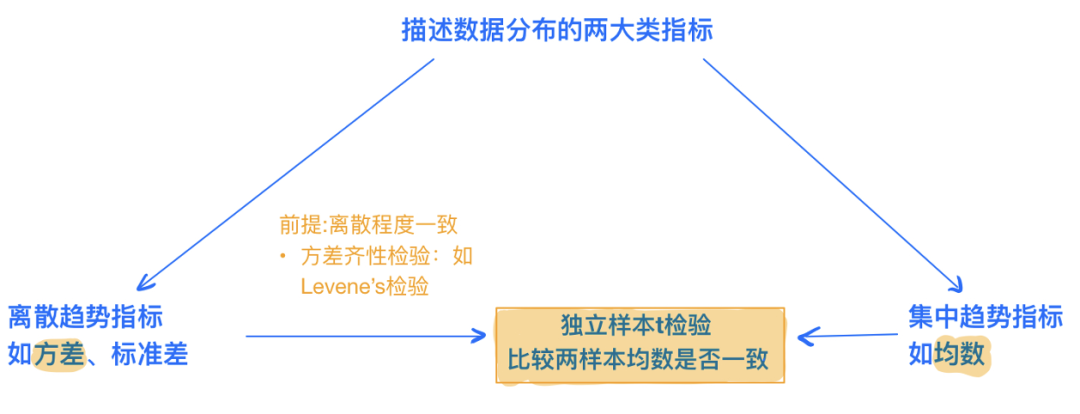
獨立樣本t檢驗是在比較兩個樣本均數是否一致，而這兩個樣本可能來源于兩個不同的分布，而離散趨勢和集中趨勢（如均數）是描述數據分布的兩大類指標。因此在確定t統計量時，我們需要考慮兩個樣本所來自的分布是否有相同的離散程度（即方差）。所以，在我們使用獨立樣本的t檢驗之前，需要先進行方差齊性檢驗（如Levene's test），查看兩個樣本來自的分布方差是否相等。
以上內容就是對t檢驗適用條件中的『正態分布』和『方差齊性』的詳細解釋。你學會了嗎？
TIPs：各位小伙伴，近日，醫咖會推出了視頻號，主要針對臨床研究過程中的常見問題進行答疑，以下為以上內容的視頻版，大家可以點擊下方視頻觀看，歡迎點贊、轉發、關注！
醫咖會面向醫生個人、醫院/單位、企業提供各種科研服務，包括研究設計、統計分析、EDC系統、科研培訓等，詳情查看：。快加小咖微信（）或掃描以下二維碼加小咖微信咨詢吧。
*請認真填寫需求信息，我們會在24小時內與您取得聯系。
